在写论文的时候,知乎上的那个答复对我帮忙颇大,从完全痴人到略微大白一点点。本着礼尚往来的精神,如今也将我所理解的隐形马尔可夫模子用尽可能通俗的语言,尽可能简单的例子,做一个讲解。
隐形马尔可夫模子,英文是 Hidden Markov Models,所以以下就简称 HMM。
既是马尔可夫模子,就必然存在马尔可夫链,该马尔可夫链从命马尔可夫性量:即无记忆性。也就是说,那一时刻的形态,受且只受前一时刻的影响,而不受更往前时刻的形态的影响。
在那里我们仍然利用十分简单的气候模子来做申明。
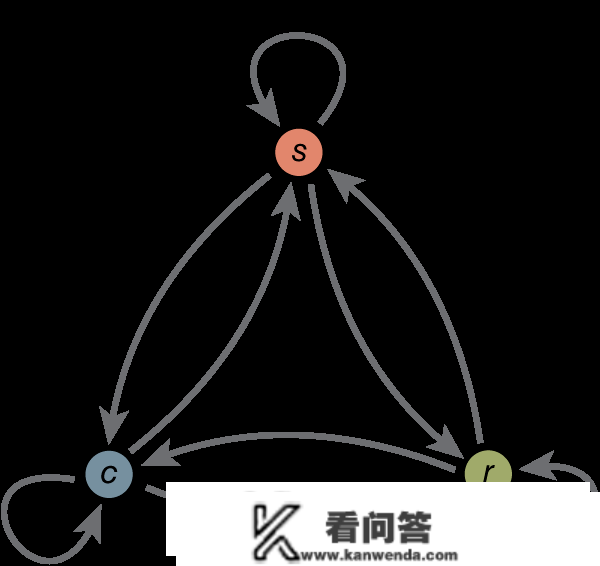
在那个马尔可夫模子中,存在三个形态,Sunny, Rainy, Cloudy,同时图片上标的是各个形态间的转移概率(若是不大白什么是转移概率,那建议先去进修什么是马尔可夫再来看HMM)。
如今我们要申明什么是 HMM。既是隐形,申明那些形态是不雅测不到的,响应的,我们能够通过其他体例来『推测』或是『揣度』那些形态,那也是 HMM 需要处理的问题之一。
举个例子,我女伴侣如今在北京工做,而我还在法国读书。每全国班之后,她会按照气候情况有响应的活动:或是去商场购物,或是去公园漫步,或是回家拾掇房间。我们有时候会通德律风,她会告诉我她那几天做了什么,而闲着没事的我呢,则要通过她的行为推测那几天对应的气候最有可能是什么样子的。
以上就是一个简单的 HMM,气候情况属于形态序列,而她的行为则属于不雅测序列。气候情况的转换是一个马尔可夫序列。而按照气候的差别,有相对应的概率产生差别的行为。在那里,为了简化,把气候情况简单归结为好天和雨天两种情况。雨天,她选择去漫步,购物,拾掇的概率别离是0.1,0.4,0.5, 而若是是好天,她选择去漫步,购物,拾掇的概率别离是0.6,0.3,0.1。而气候的转换情况如下:那一全国雨,则下一天仍然下雨的概率是0.7,而转换成好天的概率是0.3;那一天是好天,则下一天仍然是好天的概率是0.6,而转换成雨天的概率是0.4. 同时还存在一个初始概率,也就是之一全国雨的概率是0.6, 好天的概率是0.4.
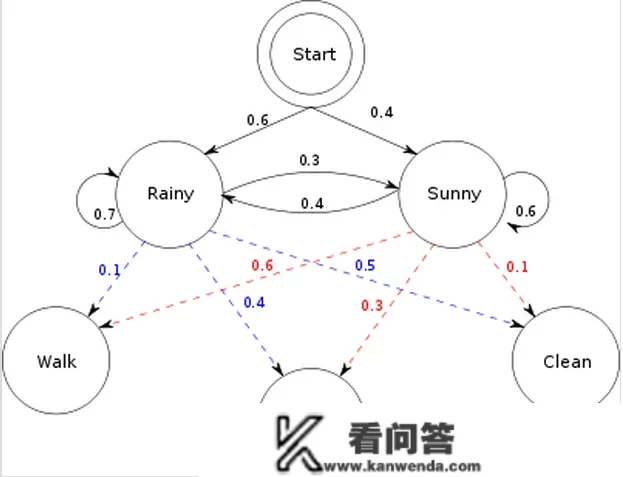
按照以上的信息,我们得到了 HMM的一些根本要素:初始概率散布 π,形态转移矩阵 A,不雅丈量的概率散布 B,同时有两个形态,三种可能的不雅测值。
如今,重点是要领会并处理HMM 的三个问题。
问题1,已知整个模子,我女伴侣告诉我,持续三天,她下班后做的工作别离是:漫步,购物,拾掇。那么,按照模子,计算产生那些行为的概率是几。
问题2,同样晓得那个模子,同样是那三件事,我女伴侣要我猜,那三天她下班后北京的气候是怎么样的。那三天怎么样的气候才最有可能让她做如许的工作。
问题3,最复杂的,我女伴侣只告诉我那三天她别离做了那三件事,而其他什么信息我都没有。她要我成立一个模子,晴雨转换概率,之一天气候情况的概率散布,按照气候情况她选择做某事的概率散布。(惨绝人寰)
而要处理那些问题,伟大的巨匠们别离找出了对应的算法。问题一,Forward Algorithm,向前算法,或者 Backward Algo,向后算法。 问题二,Viterbi Algo,维特比算法。问题三,Baum-Welch Algo,鲍姆-韦尔奇算法(中文好绕口)。
虽然例子有些荒唐(气候情况要复杂的多,并且不太可能满足马尔可夫性量;同时,女伴侣要做什么往往由表情决定而不由气候决定。而从问题一来看,必然是天数越多,那个概率就会越低;从问题三来看,察看到的行为越多,模子才气更准确一些),但是应该已经简单却又详尽地解释了什么是 HMM。若是只是想领会个大要,到此为行。
===========================我是朋分线====================================
朋分线以下的,就是详细若何处理那三大问题。需要数学根底,概率根底。
问题1的处理1:遍历算法。
要计算产生那一系列行为的概率,那我们把每一种气候情况下产生那些行为都枚举出来,那每种情况的和就是那个概率。有三天,每天有两种可能的气候情况,则总共有 2的三次=8种 情况.
举例此中一种情况 : P(下雨,下雨,下雨,漫步,购物,拾掇)=P(之一全国雨)P(之一全国雨去漫步)P(第二天接着下雨)P(下雨去购物)P(第三天还下雨)P(下雨回家拾掇)=0.6X0.1X0.7X0.4X0.7X0.5=0.00588
当然,那里面的 P(第二天接着下雨)当然是已知之一全国雨的情况下,第二全国雨的概率,为0.7.
将八种情况相加可得,三天的行为为{漫步,购物,拾掇}的可能性为0.033612. 看似简单易计算,但是一旦察看序列变长,计算量就会十分庞大(
NTN^T的复杂度,T 为不雅测序列的长度)。
问题1 的处理2:向前算法。
先计算 t=1时刻,发作『漫步』一行为的概率,若是下雨,则为 P(漫步,下雨)=P(之一全国雨)X P(漫步 | 下雨)=0.6X0.1=0.06;好天,P(漫步,好天)=0.4X0.6=0.24
t=2 时刻,发作『购物』的概率,当然,那个概率能够从 t=1 时刻计算而来。
若是t=2下雨,则 P(之一天漫步,第二天购物, 第二全国雨)= 【P(之一天漫步,之一全国雨)X P(第二全国雨 | 之一全国雨)+P(之一天漫步,之一晴和天)X P(第二全国雨 | 之一晴和天)】X P(第二天购物 | 第二全国雨)=【0.06X0.7+0.24X0.3】X0.4=0.0552
若是 t=2好天,则 P(之一天漫步,第二天购物,第二晴和天)=0.0486 (同理可得,请自行推理)
若是 t=3,下雨,则 P(之一天漫步,第二天购物,第三天拾掇,第三全国雨)=【P(之一天漫步,第二天购物,第二全国雨)X P(第三全国雨 | 第二全国雨)+ P(之一天漫步,第二天购物,第二天晴和)X P(第三全国雨 | 第二天晴和)】X P(第三天拾掇 | 第三全国雨)=【0.0552X0.7+0.0486X0.4】X0.5= 0.02904
若是t=3,好天,则 P(之一天漫步,第二天购物,第三天拾掇,第三晴和天)= 0.004572
那么 P(之一天漫步,第二天购物,第三天拾掇),那一概率则是第三天,下雨和好天两种情况的概率和。0.02904+0.004572=0.033612.
以上例子能够看出,向前算法计算了每个时间点时,每个形态的发作不雅测序列的概率,看似冗杂,但在 T 变大时,复杂度会大大降低。
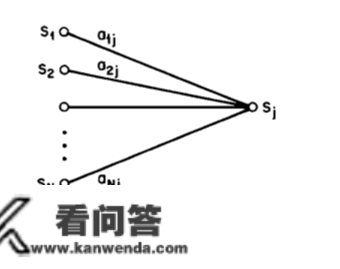
问题1的处理3:向后算法
望文生义,向前算法是在时间 t=1的时候,一步一步往前计算。而相反的,向后算法例是倒退着,从最初一个形态起头,渐渐往后推。
初始化:
β3(Rainy)=1\beta_3(Rainy)=1(之一次利用知乎的公式编纂,还蛮靠谱的嘛)
β3(Sunny)=1\beta_3(Sunny)=1递推:
β2(Rainy)=aRainy→RainybRainy(O3=Clean)β3(Rainy)+aRainy→SunnybSunny(O3=Clean)β3(Sunny)\beta_2(Rainy)=a_{Rainy\to Rainy}b_{Rainy}(O_3=Clean)\beta_3(Rainy)+a_{Rainy\to Sunny}b_{Sunny}(O_3=Clean)\beta_3(Sunny)=0,.7x0.5x1+0.3x0.1x1=0.38
此中之一项则是转移概率,第二全国雨转到第三全国雨的概率为0.7;第二项则是不雅测概率,第三全国雨的情况下,在家拾掇的概率为0.5;第三项就是我们定义的向后变量(backward variable)。
同理推得\beta_1(Rainy)=0.1298\\
\beta_1(Sunny)=0.1076" eeimg="1">
完毕:P(漫步,购物,拾掇) =
πRainybRainy(O1=Walke)β1(Rainy)+πSunnybSunny(O1=Walke)β1(Sunny)\pi_{Rainy}b_{Rainy}(O_1=Walke)\beta_1(Rainy)+\pi_{Sunny}b_{Sunny}(O_1=Walke)\beta_1(Sunny)=0.6×0.1×0.1298+0.4×0.6×0.1076
=0.033612
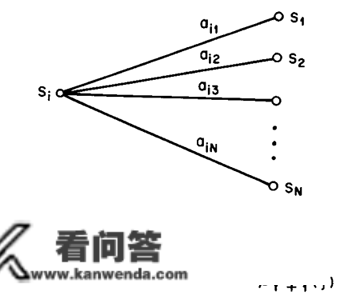
三种算法的谜底是一致的。
问题2的处理:维特比算法
维特比算法努力于寻找一条更佳途径,以便能更好地解释不雅测到的序列。
初始化:\delta_1(Sunny)=\pi_S\times b_S(O_1=Walk)=0.24" eeimg="1">
初始途径:\phi_1(Sunny)=0" eeimg="1">
递推,当然是要找出概率比力大的那条途径。
δ2(Rainy)=max[δ1(R)×aR→R,δ1(S)×aS→R]×bR(O2=Shop)=0.0384\delta_2(Rainy)=max[\delta_1(R)\times a_{R\to R},\delta_1(S)\times a_{S\to R}]\times b_R(O_2=Shop)=0.0384那么,抵达第二全国雨那一形态的更佳途径,应该是:
ϕ2(Rainy)=argmax[δ1(R)×aR→R,δ1(S)×aS→R]=Sunny\phi_2(Rainy)=\arg\max[\delta_1(R)\times a_{R\to R},\delta_1(S)\times a_{S\to R}]=Sunny也就是说,之一天是好天的可能性更大。
同样地,能够推得,\phi_2(Sunny)=Sunny\\
\delta_3(Rainy)=0.01344\\
\phi_3(Rainy)=Rainy\\
\delta_3(Sunny)=0.002592\\
\phi_3(Sunny)=Sunny
" eeimg="1">
完毕:比力
δ3(Rainy)andδ3(Sunny)\delta_3(Rainy) \quad and \quad \delta_3(Sunny)的大小,发现前者较大,则最初一天的形态最有可能是 下雨天。
回推:按照
ϕ3(Rainy)=Rainy\phi_3(Rainy)=Rainy可知,抵达第三全国雨那一形态,最有可能是第二天也下雨,再按照
ϕ2(Rainy)=Sunny\phi_2(Rainy)=Sunny可知,抵达第二全国雨那一形态,最有可能是之一天是好天。
由此,我们得到了更佳途径,即,好天,雨天,雨天。
问题3的处理:Baum-Welch 算法。
此问题的复杂度要远远高于前两种算法,不是简单解释就能说的清晰的了。如有兴趣,能够私信我。
我十分附和霍金老头的『多一个公式,少十个读者』的说法,但是本身写起来,却发现用英文的那些公式仿佛比中文更简洁易懂,中文仿佛更罗里吧嗦一些。
仍然怀着十分感恩的心,再次感激那个问题以及答复问题的那些热心的人们给我带来的帮忙。
